Kegel Volume Berekenen Ontdek de Formule en Meer

Ooit afgevraagd hoe je de inhoud van een kegelvormig object kunt berekenen? Of je nu een wiskundestudent bent, een architect, of gewoon nieuwsgierig, het berekenen van het kegelvolume is een essentiële vaardigheid. Deze gids duikt diep in de wereld van de kegel volume berekening, van de formule tot praktische toepassingen en veelgestelde vragen.

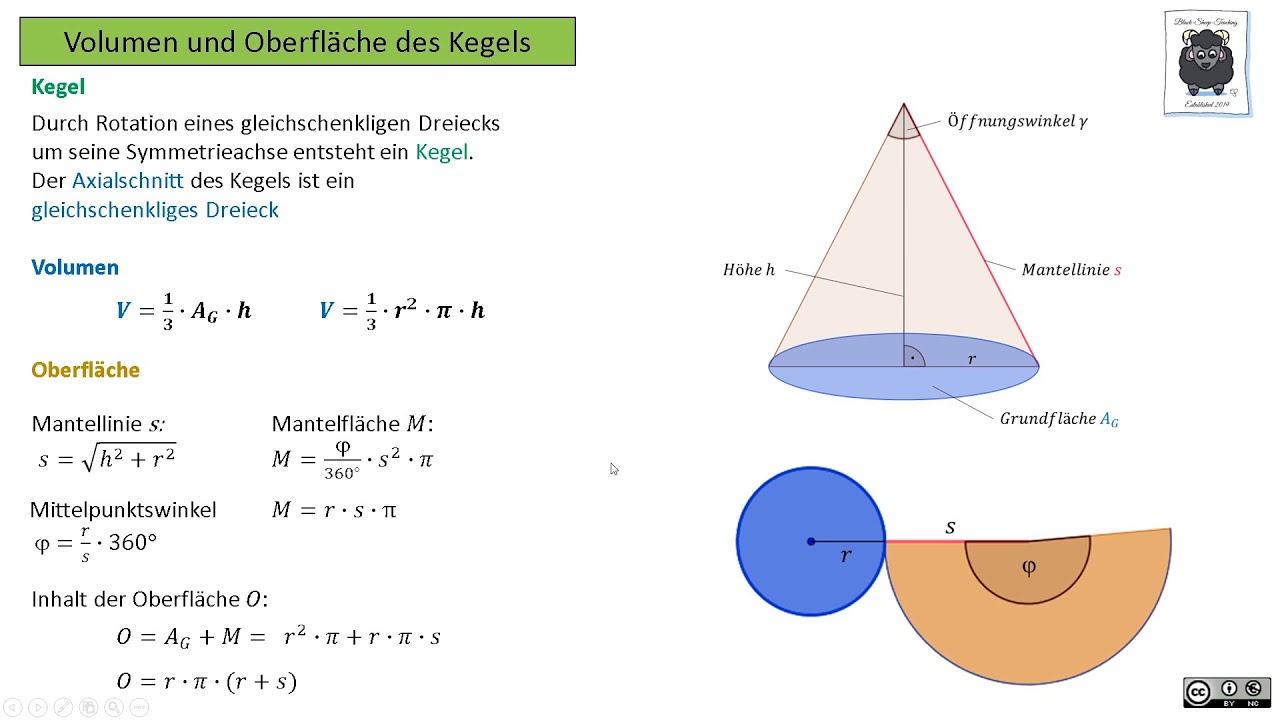
De formule voor het berekenen van het volume van een kegel is verrassend eenvoudig: 1/3 * π * r² * h. Hierbij staat 'r' voor de straal van de cirkelvormige basis van de kegel en 'h' voor de hoogte van de kegel. Maar waar komt deze formule vandaan en hoe pas je hem toe in de praktijk?

De geschiedenis van de kegel volume berekening gaat terug tot de oude Grieken. Wiskundigen zoals Archimedes hebben belangrijke bijdragen geleverd aan de ontwikkeling van deze formule. Het begrijpen van het kegelvolume is cruciaal in verschillende disciplines, van de bouwkunst tot de natuurkunde. Denk bijvoorbeeld aan het ontwerpen van silo's, het berekenen van de inhoud van een ijshoorntje of het bestuderen van vulkanische kegels.

Het belang van de formule voor kegelvolume berekenen is enorm. Het stelt ons in staat om de capaciteit van kegelvormige objecten nauwkeurig te bepalen, wat essentieel is in tal van praktische toepassingen. Stel je voor dat je een kegelvormige container moet vullen met vloeistof – zonder de juiste formule zou je de benodigde hoeveelheid niet kunnen bepalen.

Een veelvoorkomend probleem bij het berekenen van het kegelvolume is het correct meten van de straal en de hoogte. Zorg ervoor dat je de juiste meetinstrumenten gebruikt en de metingen nauwkeurig uitvoert om fouten te vermijden. Oefening baart kunst, dus probeer de formule toe te passen op verschillende voorbeelden.

Voorbeeld: Een kegel heeft een straal van 5 cm en een hoogte van 10 cm. Het volume is dan: 1/3 * π * 5² * 10 ≈ 261.8 cm³.

Voordelen van het kennen van de formule:

1. Nauwkeurige volumeberekening: Je kunt de inhoud van kegelvormige objecten precies bepalen.

2. Praktische toepassingen: Vanwege de vele toepassingen van kegelvormige objecten wordt de formule op verschillende gebieden gebruikt.

3. Vergroot inzicht in meetkunde: Begrijpen van de formule helpt bij het ontwikkelen van een dieper begrip van geometrische concepten.

Stap-voor-stap handleiding:

1. Meet de straal (r) van de cirkelvormige basis.

2. Meet de hoogte (h) van de kegel.

3. Pas de formule toe: V = 1/3 * π * r² * h.

Veelgestelde vragen:

1. Wat is de formule voor kegelvolume? V = 1/3 * π * r² * h

2. Wat is de betekenis van 'r' en 'h'? 'r' is de straal, 'h' is de hoogte.

3. Hoe meet ik de hoogte van een kegel? Van de top loodrecht naar het midden van de basis.

4. Wat is Pi (π)? Een wiskundige constante, ongeveer 3.14159.

5. Waar kan ik meer informatie vinden over kegelvolume? Zoek online naar "kegel volume berekenen formule".

6. Wat zijn enkele toepassingen van de formule? Berekenen van de inhoud van silo's, ijshoorntjes, etc.

7. Hoe kan ik de formule onthouden? Oefening en visualisatie van de kegel.

8. Wat als mijn kegel niet perfect is? Benader de metingen zo goed mogelijk.

Tips en trucs:

Gebruik een rekenmachine voor nauwkeurige berekeningen. Visualiseer de kegel om de formule beter te begrijpen.

Kortom, het berekenen van het volume van een kegel is een fundamentele vaardigheid met talloze praktische toepassingen. Door de formule 1/3 * π * r² * h te begrijpen en toe te passen, kun je de inhoud van kegelvormige objecten nauwkeurig bepalen. Of je nu een student, professional of gewoon nieuwsgierig bent, het beheersen van deze formule is een waardevolle aanwinst. Het begrijpen van geometrische principes zoals het berekenen van het kegelvolume opent deuren naar een dieper begrip van de wereld om ons heen. Blijf oefenen met verschillende voorbeelden en je zult zien dat het berekenen van kegelvolumes een fluitje van een cent wordt! Vergeet niet de formule V = 1/3 * π * r² * h en ga aan de slag!

Spookachtige apps ontdekken de ultieme gids
Anna van saksenlaan 50 den haag ontdek de charme van deze locatie
De betekenis van betekenis ontdek de kracht van interpretatie