Maîtriser le Calcul des Quartiles en Statistique

Dans le monde fascinant de l'analyse de données, la compréhension des quartiles est essentielle. Mais comment calculer un quartile en statistique et pourquoi est-ce si important ? Cet article vous guidera à travers les méandres de cette notion statistique, en vous fournissant les outils nécessaires pour la maîtriser.
Imaginez que vous analysez les salaires d'une entreprise. Vous voulez comprendre la distribution des revenus, identifier les valeurs centrales et repérer d'éventuelles disparités. C'est là que le calcul des quartiles entre en jeu. En découpant la distribution en quatre parts égales, les quartiles offrent une vision claire de la répartition des données.
La détermination des quartiles trouve ses racines dans les travaux pionniers de Francis Galton au 19ème siècle. Il cherchait des méthodes pour analyser et interpréter les données de manière plus efficace. Depuis, le calcul des quartiles est devenu un outil indispensable en statistique descriptive, permettant de synthétiser l'information et de faciliter la prise de décision.
L'importance de savoir comment déterminer un quartile en statistique est indéniable. Il permet d'identifier les valeurs atypiques, de comparer des distributions et de mieux comprendre la dispersion des données. Toutefois, une mauvaise interprétation des quartiles peut conduire à des conclusions erronées. Il est donc crucial de bien maîtriser cette technique.
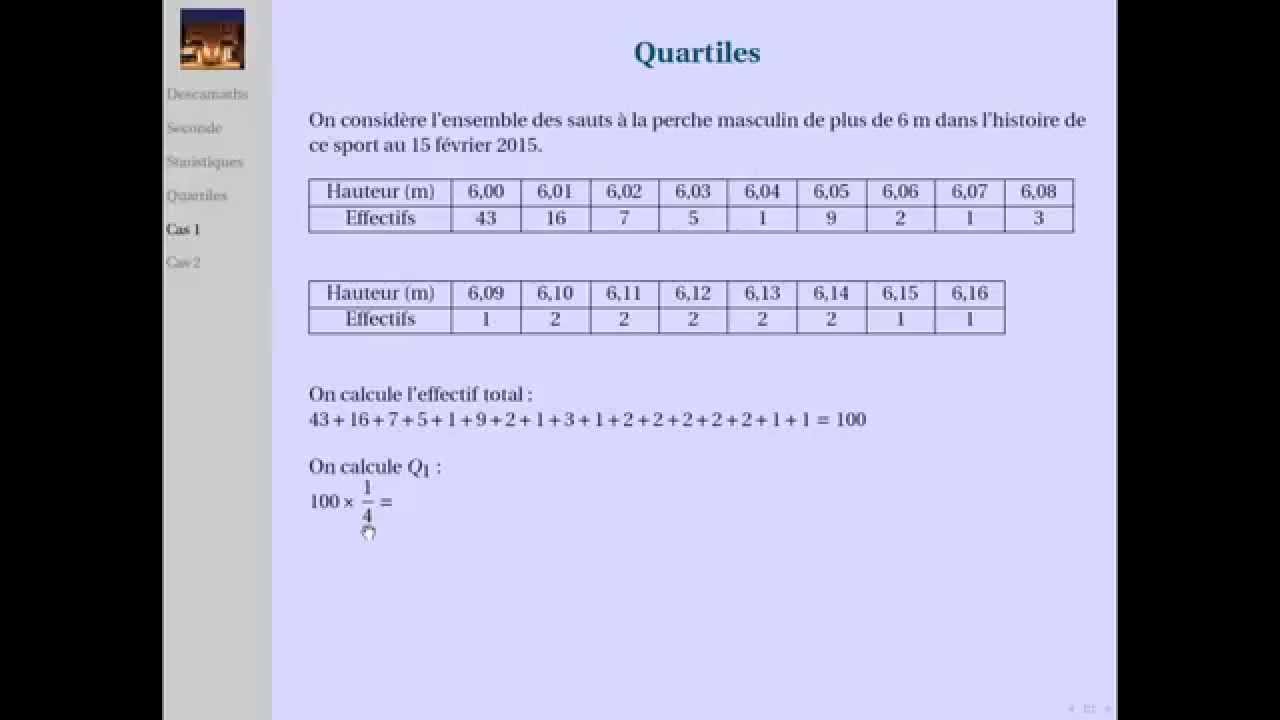
Un quartile divise un ensemble de données ordonnées en quatre parties égales. Le premier quartile (Q1) représente la valeur en dessous de laquelle se trouvent 25% des données. Le deuxième quartile (Q2), aussi appelé médiane, représente la valeur centrale de la distribution. Le troisième quartile (Q3) représente la valeur en dessous de laquelle se trouvent 75% des données.
Pour calculer les quartiles, il faut d'abord ordonner les données. Ensuite, on utilise des formules spécifiques pour déterminer les positions de Q1 et Q3. Par exemple, pour un ensemble de données de taille n, la position de Q1 est (n+1)/4. Si le résultat est un nombre entier, Q1 est la valeur à cette position. Si le résultat est un nombre décimal, on utilise une interpolation linéaire entre les valeurs adjacentes.
Exemple : Pour les données {2, 4, 6, 8, 10}, Q1 est à la position (5+1)/4 = 1.5. Q1 est donc la moyenne entre 2 et 4, soit 3. Q3 est à la position 3*(5+1)/4 = 4.5, soit la moyenne entre 8 et 10, donc 9.
Avantages du calcul des quartiles : 1. Identification des valeurs extrêmes. 2. Comparaison de distributions. 3. Calcul de l'écart interquartile (IQR), une mesure de dispersion robuste.
Étapes pour calculer un quartile: 1. Ordonner les données. 2. Calculer la position du quartile. 3. Déterminer la valeur du quartile.
Avantages et Inconvénients du Calcul des Quartiles
Meilleures pratiques : 1. Vérifier la qualité des données. 2. Choisir la méthode de calcul appropriée. 3. Interpréter les résultats avec prudence.
Exemples concrets : Analyse des revenus, des notes d'examens, des performances sportives.
Défis et solutions : Données manquantes, valeurs aberrantes, interprétation des résultats.
FAQ : Qu'est-ce qu'un quartile ? Comment interpréter les quartiles ? Quelle est la différence entre un quartile et un percentile ?
Conseils et astuces : Utiliser des logiciels statistiques, se familiariser avec les différentes méthodes de calcul.
En conclusion, comprendre comment calculer un quartile en statistique est une compétence précieuse pour tout analyste de données. Les quartiles permettent d'explorer les données en profondeur, de révéler des tendances cachées et de prendre des décisions éclairées. En maîtrisant cette technique, vous pourrez transformer des données brutes en informations pertinentes et exploitables. Alors, n'hésitez plus, explorez le monde fascinant des quartiles et optimisez votre analyse de données dès aujourd'hui !
Decryptage du mystere du quart tout ce que vous devez savoir
Decouvrir porte de clignancourt metro votre guide complet
Combien de temps vit un chat secrets dune longue vie feline