Déchiffrer le Mystère des Diviseurs en Mathématiques

Vous êtes-vous déjà demandé ce qui se cache derrière le terme "diviseur" en mathématiques ? Ce concept, apparemment simple, est fondamental pour comprendre de nombreux autres aspects des mathématiques, de l'arithmétique élémentaire à l'algèbre avancée. Dans cet article, nous allons explorer en profondeur la signification d'un diviseur, dévoiler ses mystères et illustrer son importance.
Un diviseur d'un nombre entier est un autre nombre entier qui divise le premier nombre sans laisser de reste. Par exemple, 2 est un diviseur de 10 car 10 divisé par 2 égale 5, sans reste. Comprendre cette notion est crucial pour travailler avec les fractions, les proportions, et même pour résoudre des équations.
L'histoire des diviseurs remonte à l'Antiquité, avec des mathématiciens comme Euclide qui ont exploré les propriétés des nombres et de la divisibilité. La recherche des diviseurs d'un nombre est un problème fondamental en théorie des nombres, et a mené à des découvertes importantes, comme le crible d'Ératosthène pour trouver les nombres premiers. L'importance des diviseurs se reflète également dans des domaines comme la cryptographie, où la factorisation de grands nombres en leurs diviseurs premiers joue un rôle crucial.
Un problème courant lié à la notion de diviseur est la confusion entre diviseur et multiple. Il est important de se rappeler qu'un diviseur est un nombre qui divise un autre nombre, tandis qu'un multiple est le résultat de la multiplication d'un nombre par un entier. Par exemple, 5 est un diviseur de 15, et 15 est un multiple de 5.
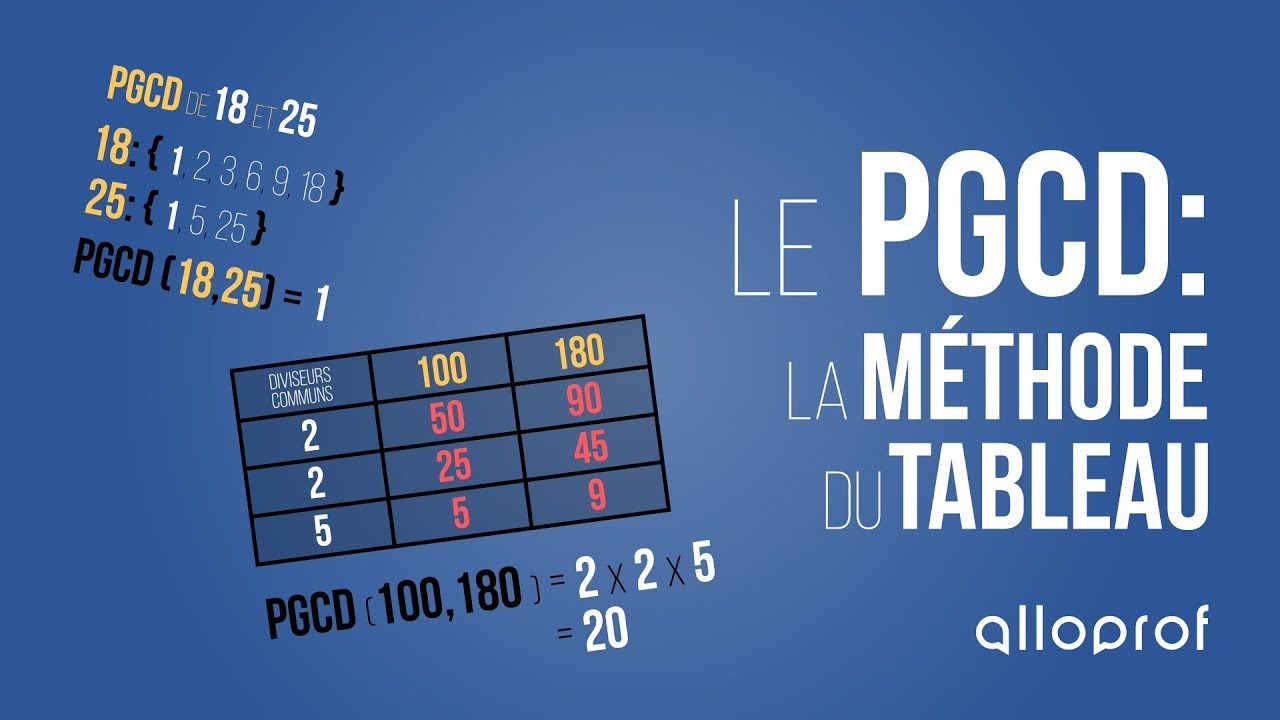
La compréhension des diviseurs est essentielle pour simplifier les fractions. En trouvant le plus grand commun diviseur (PGCD) du numérateur et du dénominateur, on peut réduire une fraction à sa forme la plus simple. Par exemple, le PGCD de 12 et 18 est 6, donc la fraction 12/18 peut être simplifiée à 2/3.
Un autre avantage de la maîtrise des diviseurs est la facilité de travailler avec les proportions et les ratios. En comprenant les diviseurs communs, on peut simplifier les ratios et les exprimer sous leur forme la plus simple.
Pour trouver les diviseurs d'un nombre, on peut utiliser la méthode de la division successive. Par exemple, pour trouver les diviseurs de 12, on divise 12 par 1, 2, 3, 4, 6 et 12. Tous ces nombres divisent 12 sans laisser de reste, donc ce sont les diviseurs de 12.
Avantages et Inconvénients de la Connaissance des Diviseurs
Il n'y a pas vraiment d'inconvénients à connaître les diviseurs. C'est une connaissance fondamentale en mathématiques.
Voici quelques exemples concrets d'utilisation des diviseurs : simplification de fractions (12/18 = 2/3), détermination de si un nombre est pair ou impair (tous les nombres pairs sont divisibles par 2), calcul du PGCD pour simplifier des ratios (15 : 25 = 3 : 5), et la factorisation en nombres premiers (12 = 2 x 2 x 3).
Questions fréquemment posées :
1. Qu'est-ce qu'un diviseur ? Réponse : Un diviseur est un nombre qui divise un autre nombre sans laisser de reste.
2. Comment trouver les diviseurs d'un nombre ? Réponse : Par division successive.
3. Quelle est la différence entre un diviseur et un multiple ? Réponse : Un diviseur divise un nombre, un multiple est le résultat d'une multiplication.
4. Pourquoi les diviseurs sont-ils importants ? Réponse : Ils sont essentiels pour comprendre les fractions, les proportions, etc.
5. Qu'est-ce que le PGCD ? Réponse : Le Plus Grand Commun Diviseur.
6. Comment simplifier une fraction ? Réponse : En divisant le numérateur et le dénominateur par leur PGCD.
7. Comment savoir si un nombre est un diviseur d'un autre nombre ? Réponse : En effectuant la division et en vérifiant si le reste est nul.
8. Quel est le lien entre les diviseurs et les nombres premiers ? Réponse : Les nombres premiers n'ont que deux diviseurs : 1 et eux-mêmes.
En conclusion, la compréhension du concept de diviseur est fondamentale en mathématiques. De la simplification des fractions à la résolution de problèmes complexes, les diviseurs jouent un rôle essentiel. En maîtrisant ce concept, vous ouvrez la porte à une meilleure compréhension des nombres et de leurs relations, vous permettant de naviguer avec aisance dans le monde fascinant des mathématiques. Alors, n'hésitez pas à explorer davantage les diviseurs et à approfondir vos connaissances !
Selles jaunes mystere resolu decryptage couleur caca
Communaute et spiritualite a montigny le bretonneux
Heures de priere a saint priest un guide complet