Grenzkostenfunktion bestimmen mit Analysis

Stellen Sie sich vor, Sie könnten den genauen Punkt bestimmen, an dem Ihre Produktionskosten am effizientesten sind. Dieser Punkt, an dem jede zusätzliche Einheit am günstigsten produziert wird, ist der Schlüssel zur Gewinnmaximierung. Die Berechnung der Grenzkostenfunktion mithilfe der Analysis liefert Ihnen genau diese Information. Dieser Artikel taucht tief in die Welt der Grenzkosten ein und bietet Ihnen das notwendige Wissen, um dieses mächtige Werkzeug zu beherrschen.

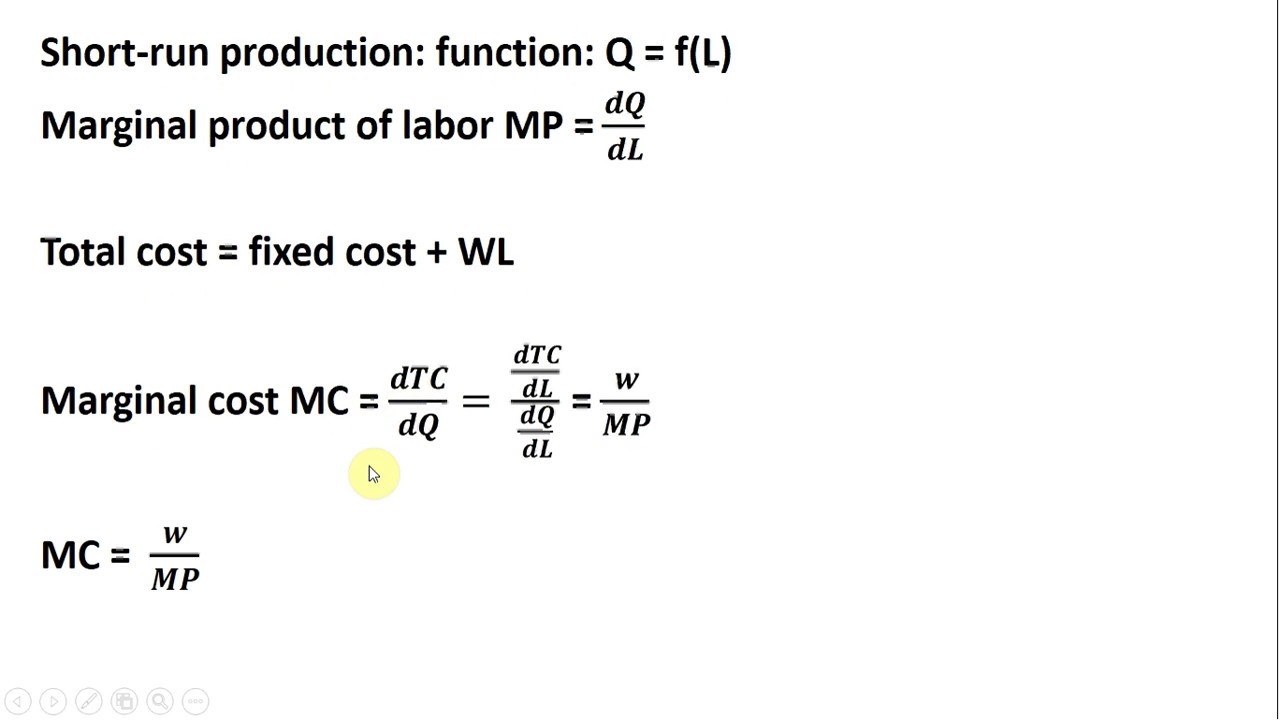
Die Grenzkostenfunktion, ein Kernkonzept der Mikroökonomie, beschreibt die zusätzlichen Kosten, die bei der Produktion einer weiteren Einheit eines Gutes entstehen. Die Berechnung dieser Funktion erfordert den Einsatz der Differentialrechnung, genauer gesagt, die Ableitung der Gesamtkostenfunktion. Durch die Analyse der Grenzkosten können Unternehmen fundierte Entscheidungen über Produktionsmengen und Preisgestaltung treffen.

Die mathematische Grundlage für die Bestimmung der Grenzkostenfunktion liegt in der Beziehung zwischen Kosten und Produktionsmenge. Die Gesamtkostenfunktion, oft als K(x) bezeichnet, repräsentiert die Gesamtkosten für die Produktion von x Einheiten eines Gutes. Die Grenzkostenfunktion, bezeichnet als K'(x), ist die Ableitung der Gesamtkostenfunktion nach x. Sie gibt die Änderungsrate der Gesamtkosten in Bezug auf die Produktionsmenge an.

Historisch betrachtet entstand das Konzept der Grenzkosten im Zuge der Industrialisierung und dem wachsenden Bedarf an effizienteren Produktionsmethoden. Die frühen Ökonomen erkannten die Bedeutung der Analyse der Kostenstruktur, um die optimale Produktionsmenge zu bestimmen. Die Entwicklung der Differentialrechnung lieferte das mathematische Werkzeug, um die Grenzkosten präzise zu berechnen und ihre Auswirkungen auf die Gewinnmaximierung zu untersuchen.

Ein Hauptproblem bei der Anwendung der Grenzkostenfunktion in der Praxis ist die genaue Bestimmung der Gesamtkostenfunktion. In realen Szenarien können die Kosten von verschiedenen Faktoren beeinflusst werden, die schwer zu quantifizieren sind. Vereinfachte Modelle können helfen, die Komplexität zu reduzieren, aber sie bieten möglicherweise keine vollständig realistische Darstellung der tatsächlichen Kostenstruktur.

Die Grenzkostenfunktion K'(x) wird durch die Ableitung der Gesamtkostenfunktion K(x) berechnet. Ist beispielsweise K(x) = x³ + 2x² + 5x + 10, dann ist K'(x) = 3x² + 4x + 5. Diese Funktion gibt die Grenzkosten für jede Produktionsmenge x an.

Vorteile der Grenzkostenanalyse:

1. Gewinnmaximierung: Durch den Vergleich der Grenzkosten mit dem Grenzerlös lässt sich die optimale Produktionsmenge bestimmen, bei der der Gewinn maximiert wird.

2. Effizienzsteigerung: Die Analyse der Grenzkosten hilft, Ineffizienzen im Produktionsprozess zu identifizieren und zu beseitigen.

3. Fundierte Preisgestaltung: Die Grenzkosten dienen als Grundlage für die Preisgestaltung und ermöglichen es, wettbewerbsfähige Preise festzulegen.

Aktionsplan zur Bestimmung der Grenzkosten:

1. Ermitteln Sie die Gesamtkostenfunktion.

2. Berechnen Sie die Ableitung der Gesamtkostenfunktion.

3. Analysieren Sie die Grenzkostenfunktion, um die optimale Produktionsmenge zu bestimmen.

Häufig gestellte Fragen:

1. Was sind Grenzkosten? - Die Kosten für die Produktion einer weiteren Einheit.

2. Wie berechnet man die Grenzkostenfunktion? - Durch Ableitung der Gesamtkostenfunktion.

3. Wozu dient die Grenzkostenfunktion? - Zur Bestimmung der optimalen Produktionsmenge.

4. Was ist der Zusammenhang zwischen Grenzkosten und Gewinnmaximierung? - Gewinn ist maximal, wenn Grenzkosten gleich Grenzerlös sind.

5. Welche Herausforderungen gibt es bei der Anwendung der Grenzkostenanalyse? - Die genaue Bestimmung der Gesamtkostenfunktion kann schwierig sein.

6. Welche Rolle spielt die Analysis bei der Berechnung der Grenzkosten? - Die Ableitung ist ein zentraler Bestandteil der Berechnung.

7. Wie können Unternehmen die Grenzkostenanalyse in der Praxis nutzen? - Zur Optimierung der Produktion und Preisgestaltung.

8. Gibt es Software zur Berechnung der Grenzkosten? - Ja, verschiedene Tabellenkalkulationsprogramme und spezielle Softwarelösungen können verwendet werden.

Tipps und Tricks:

Vereinfachen Sie die Gesamtkostenfunktion, falls notwendig, um die Berechnung der Ableitung zu erleichtern. Nutzen Sie Software oder Online-Rechner zur Unterstützung bei der Berechnung der Ableitung.

Die Grenzkostenfunktion ist ein unverzichtbares Werkzeug für Unternehmen, die ihre Produktion optimieren und ihren Gewinn maximieren möchten. Die Kenntnis der mathematischen Grundlagen und die Fähigkeit, die Grenzkostenfunktion zu interpretieren, ermöglicht es, fundierte Entscheidungen zu treffen und im Wettbewerb erfolgreich zu agieren. Durch die Anwendung der hier beschriebenen Prinzipien und Techniken können Unternehmen die Vorteile der Grenzkostenanalyse voll ausschöpfen und ihre Wirtschaftlichkeit nachhaltig verbessern. Die Beherrschung der Grenzkostenanalyse ist ein wichtiger Schritt auf dem Weg zu einer effizienten und profitablen Unternehmensführung. Nutzen Sie dieses Wissen, um Ihre Wettbewerbsfähigkeit zu stärken und Ihr Unternehmen auf die nächste Stufe zu heben. Die Investition in das Verständnis und die Anwendung dieses Konzepts zahlt sich langfristig aus und trägt maßgeblich zum Erfolg Ihres Unternehmens bei.

Die sehnsucht nach dem eigentlichen ich will meine ruhe
Lego dampfzug bauanleitungen entdecke den ultimativen guide
Milla und caro bei berlin tag nacht freundschaft drama und grossstadtleben